本文出自:【InTheWorld的博客】 (欢迎留言、交流)
近几年来,VR型的多媒体变得越来越常见。在YouTube上就有很多360度视频,很多地图产品也提供全景街道图。作为开发者,我们不禁要想如何实现多媒体的全景渲染呢?
其实,渲染VR的多媒体其实并不难,这里就以360度视频为例介绍一下。我也没有尝试过从头写一个360视频渲染库(目前能力和精力都不太允许),所以这篇博客其实是基于开源库的——https://github.com/ashqal/MD360Player4Android。此外,我不准备详细去介绍这个库怎么使用,而是基于它分析整个渲染流程。
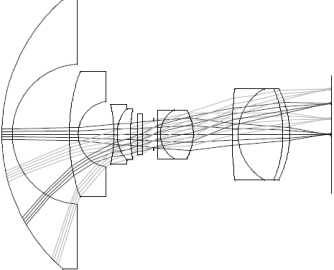
全景视频一般由鱼眼镜头产生,鱼眼镜头的物理结构大致如下:
最左边的就是一个曲面的镜头,光线就是从这里进入相机的。然后,光线经过一系列的光学结构,最终会映射到最右边的成像面上,也就是CMOS传感器阵列上。从图中可以看出,边缘的光线会被压缩,这是广视角导致的。下面这张图可以非常直观的体现这种图像映射关系。
物理世界的平面网格在鱼眼镜头中会被成像为图中这种形式,可以明显看到边缘图像被压缩了。如果把鱼眼镜头的成像看做“三维到平面的映射”,那么360度多媒体渲染就是“平面到三维的映射”。而在OpenGL中,“平面图像到三维的映射”有一个专有名词——贴图。所以接下来,我们就来分析如何通过OpenGL ES在Andorid上实现360度图像渲染。这个过程会用到不少的OpenGL知识,所以我只能假设你已经具备这些知识了。如果不是的话,我建议去读一读《OpenGL ES应用开发指南》,其他OpenGL(非ES)的书也是可以的,基础知识点是差不多的。
平面到三维的映射——贴图
无论是视频还是图像,在图像渲染阶段都是一样的,都是把一帧图像贴到一个三维模型上。所以我们从这里开始分析吧!由于仅仅是贴图,所以shader的代码还是很简单的,我简单的把顶点着色和片段着色的代码贴到下面!
uniform mat4 u_MVPMatrix; // A constant representing the combined model/view/projection matrix.
uniform mat4 u_STMatrix;
uniform bool u_UseSTM;
attribute vec4 a_TexCoordinate; // Per-vertex texture coordinate information we will pass in.
varying vec2 v_TexCoordinate; // This will be passed into the fragment shader.
void main()
{
// Transform the vertex into eye space.
v_Position = vec3(u_MVMatrix * a_Position);
// Pass through the texture coordinate.
if(u_UseSTM){
v_TexCoordinate = (u_STMatrix * a_TexCoordinate).xy;
} else {
v_TexCoordinate = a_TexCoordinate.xy;
}
gl_Position = u_MVPMatrix * a_Position;
}
这个vertex shader的代码非常简单,u_MVPMatrix就是最重要的投影变换矩阵,u_STMatrix和u_STMatrix的作用本来是为了实现Texture的变换,但实际上这不是必须的,所以可以忽略这两个参数。u_MVPMatrix这个矩阵实现了模型坐标系—>观测坐标系—>投影平面的变换,具体的逻辑就不细说了,有很多资料可以查阅。
至于片段作色器,更是简单到没朋友了,如下:
#extension GL_OES_EGL_image_external : require
precision mediump float;
uniform samplerExternalOES u_Texture;
varying vec2 v_TexCoordinate; // Interpolated texture coordinate per fragment.
void main()
{
gl_FragColor = texture2D(u_Texture, v_TexCoordinate);
}
这个片段作色器就是很简单的把贴图映射到模型的点上,没有很多东西要讲。把两个作色器的代码贴出来的一个重要目的就是让大家知道这里对OpenGL的要求其实非常之低。
既然glsl的代码如此简单,可以断定Renderer的代码也应该不难。MD360Player4Android这个项目的render实现类为MD360Renderer,MD360Renderer中包含了很多的Plugin,不同的plugin组合起来完成各种不同的工作。其中最重要的plugin被称为mainPlugin,而这个最重要的Plugin的任务其实就是完成模型贴图的映射。这个mainPlugin是由ProjectionModeManager构造的,它本身相当于一个工厂类,负责构造不同的映射模式。不同的映射模式在视觉上的区别比较大,但是原理上却都是非常接近的。这里以Dome模式为例分析其实现原理,dome模式就是把图像映射到一个球体上,然后在球心位置观察这个模型。DomeProjection的源代码如下:
public class DomeProjection extends AbsProjectionStrategy {
MDAbsObject3D object3D;
private float mDegree;
private boolean mIsUpper;
private RectF mTextureSize;
public DomeProjection(RectF textureSize, float degree, boolean isUpper) {
this.mTextureSize = textureSize;
this.mDegree = degree;
this.mIsUpper = isUpper;
}
@Override
public void turnOnInGL(Context context) {
object3D = new MDDome3D(mTextureSize, mDegree, mIsUpper);
MDObject3DHelper.loadObj(context, object3D);
}
@Override
public MDAbsObject3D getObject3D() {
return object3D;
}
@Override
public MDAbsPlugin buildMainPlugin(MDMainPluginBuilder builder) {
return new MDPanoramaPlugin(builder);
}
}
从简短的代码中可以看出,这个类做的事情也不多,主要是通过MDDome3D这个类构造出了一个模型。所有关键的细节都还是要到MDDome3D的代码中来研究,话不多说,继续上代码了!MDDome3D的代码虽然也有150行,但关键的函数其实就是generateDome();
public static void generateDome(float radius, int sectors, float degreeY, boolean isUpper, MDDome3D object3D) {
final float PI = (float) Math.PI;
final float PI_2 = (float) (Math.PI / 2);
float percent = degreeY / 360;
int rings = sectors >> 1;
float R = 1f/rings;
float S = 1f/sectors;
short r, s;
float x, y, z;
int lenRings = (int) (rings * percent) + 1;
int lenSectors = sectors + 1;
int numPoint = lenRings * lenSectors;
float[] vertexs = new float[numPoint * 3];
float[] texcoords = new float[numPoint * 2];
short[] indices = new short[numPoint * 6];
int upper = isUpper ? 1 : -1;
int t = 0, v = 0;
for(r = 0; r < lenRings; r++) {
for(s = 0; s < lenSectors; s++) {
x = (float) (Math.cos( 2 * PI * s * S ) * Math.sin( PI * r * R )) * upper;
y = (float) Math.sin( -PI_2 + PI * r * R ) * -upper;
z = (float) (Math.sin( 2 * PI * s * S ) * Math.sin( PI * r * R ));
float a = (float) (Math.cos( 2 * PI * s * S) * r * R / percent)/2.0f + 0.5f;
float b = (float) (Math.sin( 2 * PI * s * S) * r * R / percent)/2.0f + 0.5f;
texcoords[t++] = b;
texcoords[t++] = a;
vertexs[v++] = x * radius;
vertexs[v++] = y * radius;
vertexs[v++] = z * radius;
}
}
int counter = 0;
for(r = 0; r < lenRings - 1; r++){
for(s = 0; s < lenSectors - 1; s++) {
indices[counter++] = (short) (r * lenSectors + s); //(a)
indices[counter++] = (short) ((r+1) * lenSectors + (s)); //(b)
indices[counter++] = (short) ((r) * lenSectors + (s+1)); // (c)
indices[counter++] = (short) ((r) * lenSectors + (s+1)); // (c)
indices[counter++] = (short) ((r+1) * lenSectors + (s)); //(b)
indices[counter++] = (short) ((r+1) * lenSectors + (s+1)); // (d)
}
}
// initialize vertex byte buffer for shape coordinates
ByteBuffer bb = ByteBuffer.allocateDirect(
// (# of coordinate values * 4 bytes per float)
vertexs.length * 4);
bb.order(ByteOrder.nativeOrder());
FloatBuffer vertexBuffer = bb.asFloatBuffer();
vertexBuffer.put(vertexs);
vertexBuffer.position(0);
// initialize vertex byte buffer for shape coordinates
ByteBuffer cc = ByteBuffer.allocateDirect(
texcoords.length * 4);
cc.order(ByteOrder.nativeOrder());
FloatBuffer texBuffer = cc.asFloatBuffer();
texBuffer.put(texcoords);
texBuffer.position(0);
// initialize byte buffer for the draw list
ByteBuffer dlb = ByteBuffer.allocateDirect(
// (# of coordinate values * 2 bytes per short)
indices.length * 2);
dlb.order(ByteOrder.nativeOrder());
ShortBuffer indexBuffer = dlb.asShortBuffer();
indexBuffer.put(indices);
indexBuffer.position(0);
object3D.setIndicesBuffer(indexBuffer);
object3D.setTexCoordinateBuffer(0,texBuffer);
object3D.setTexCoordinateBuffer(1,texBuffer);
object3D.setVerticesBuffer(0,vertexBuffer);
object3D.setVerticesBuffer(1,vertexBuffer);
object3D.setNumIndices(indices.length);
object3D.texCoordinates = texcoords;
}
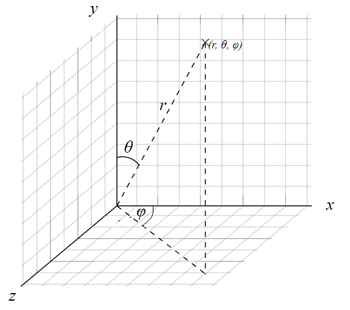
这个函数的功能是构造模型,而这个模型主要的数据就是顶点坐标、纹理坐标和顶点索引。顶点坐标数组和纹理坐标是一一对应的关系,而顶点索引则是为了为OpenGL提供渲染单元,在这里是一个个三角形。它们分别对应程序中的vertexs, texcoords以及indices。vertexs与texcoords的关系就是球体到平面的映射关系,你可以把这种关系想象成把一个薄壳球体压平形成了一个平面。可能这样讲还是有点糊涂,看代码也不容易看清楚,看图的话会相对容易理解一些。
如上图所示,使用球极坐标来描述映射关系。这里的θ就是Pi * r * R ,而φ就是2 * Pi * s * S。所以有如下直角坐标坐标与球坐标的关系:
而球坐标与平面坐标的关系更为直白,其中值得注意的一点是单个鱼眼镜头的视角是达不到360度的。所以在计算对应贴图坐标的时候,增加了percent这个变量。而最后(a, b)的坐标需要加上一个(0.5, 0.5)的偏移量是为了把球坐标圆心映射到贴图的中心。至于indices的构成,其实更容易理解了,只要基于球坐标的映射关系理解即可。
至此,dome模式的映射就完成了。当然,还是有很多细节没有分析,但是碍于篇幅,这些内容就留到以后了。我们先来看看效果吧!首先是原图,如下,
然后是dome映射模式的效果,如下所示。虽然这里只展示了一张图片,但事实上渲染360度的视频是非常类似的。而且,由于Android上有GLSurfaceTexture的存在,会比其他平台更加方便。
对于以上内容的有疑问和兴趣的同学,欢迎留言、讨论!


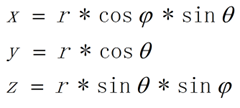


发表评论