本文出自:【InTheWorld的博客】 (欢迎留言、交流)
写在前面
学习量子力学是几年前立的Flag了,一直没有真正投入时间。主要的原因还是“要吃饭”,而且一些层出不穷的新技术也有点迷惑了我。不过本质上还是自己科学品味太差,二来加上意志力不够坚定。目前已经花了一段时间学量子力学、量子信息,写在这里权当做笔记吧!
Deutsch-Jozsa算法问题
Deutsch-Jozsa是一个简单的量子算法例子。虽然从实用角度讲,这个算法意义不大,但是却能很好的体现量子计算的优越性。首先是问题的描述: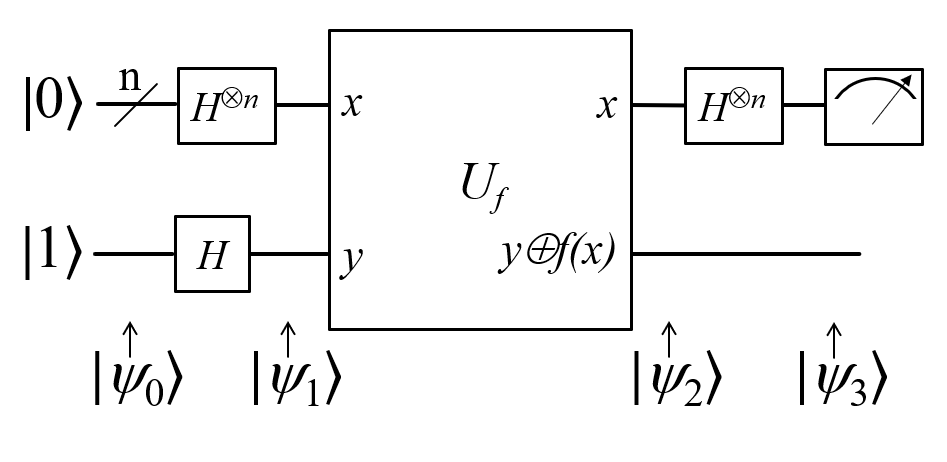
考虑一个黑盒子,我们称为oracle。它可以计算一个比特的布尔函数。每做一次计算,我们就称为是
对oracle的一次查询。对于这个函数,存在以下四种可能:
| 输入 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|
| 输出 | 1 | 0 | 0 | 1 |
第(1,4)列或者(2,3)列组合而成的情况,我们称oracle为常数函数;第(1,2)列,或者(3,4)列组合而成的情况,我们称之为平衡函数。Deutsch问题可如下表述:对于这样一个函数,如何通过对oracle的查询,确定它是常数函数还是平衡函数?
在经典算法里,我们使用经典比特来进行计算。为了确定单比特函数的类型,我们至少要对oracle进行两次的查询。如果输入是n bit长度,则需要2^{n-1}+1次。但是对于量子算法而言,只需要一次调用oracle就能判断出结果。
算法过程描述如下:
1. \vert 0 \rangle^{\bigotimes n}\vert 1 \rangle; 初始化状态
2. \dfrac{1}{\sqrt{2^n}} \displaystyle\sum_{x=0}^{2^n-1} \vert x \rangle [\frac {\vert 0 \rangle - \vert 1 \rangle}{\sqrt{2}}]; 使用Hadamard门生成叠加态
3. \displaystyle\sum_{x}^{} (-1)^{f(x)} \vert x \rangle [\frac {\vert 0 \rangle - \vert 1 \rangle}{\sqrt{2}}]; 通过oracle函数以及异或变换
4. \displaystyle\sum_{z}{} \sum_{x}^{} \dfrac{(-1)^{x \cdot z + f(x)}}{\sqrt{2^n}} \vert z \rangle [\frac {\vert 0 \rangle - \vert 1 \rangle}{\sqrt{2}}];再次通过Hadamard门变换
5. 测量z的值,如果z为0,则说明f是常数函数
Deutsch-Jozsa算法推导
- 第二个步骤中,其实也很好理解,\vert 0 \rangle量子态通过Hadamard门之后,会变成\dfrac {\vert 0 \rangle + \vert 1 \rangle}{\sqrt{2}}。而且n个bit的情况都是基本一样的,因此张量积其实也很好改写,用x这个从0 \rightarrow {2^n -1}的数表示就行。
-
第三个步骤中,其中的变换就是U_f:{\vert x,y \rangle} \rightarrow \vert x, y \bigoplus f ( x ) \rangle;这里可以使用真值表的方式来推导:
| y \bigoplus f ( x ) | y=0 | y=1 |
|---|---|---|
| f(x) = 0 | 0 | 1 |
| f(x) = 1 | 1 | 0 |
因为f(x)只有两个取值(0或者1),所以量子状态可以写成步骤3中的形式。
- 第四个步骤中,首先要明确x \cdot z的含义是按位与再相加。容易知道,选定一个态z, 任何的态x都有相同的比例转换为z。这是由于Hadamard门的性质导致的,但是Hadamard门还有一个性质就是,\vert 1 \rangle变换后为态\dfrac {\vert 0 \rangle - \vert 1 \rangle}{\sqrt{2}}是带一个正负。也就是说,x和z的某一同时为1,则张量积的符号位会翻转一次。所以就会出现步骤4中的形式。
- 最后考虑观测;观测前分析一下,z为0的情况,如果f(x)也是常数函数,则该态的幅值为1;如果f(x)为平衡函数,则该态的幅值为0,正负号相抵消了。而且考虑到这是一个离散概率分布,概率为零意味着理论上这件事绝对不会发生。
基于IBM量子计算平台的实验
- 首先是平衡函数的情况
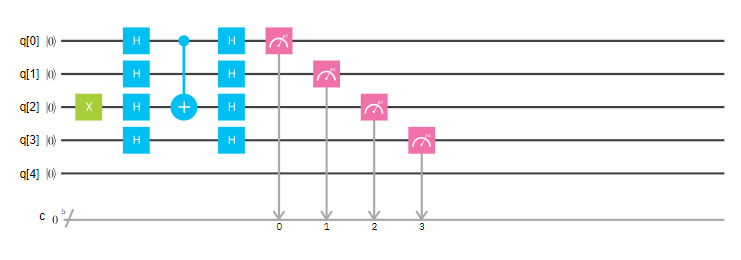
其运行结果是:
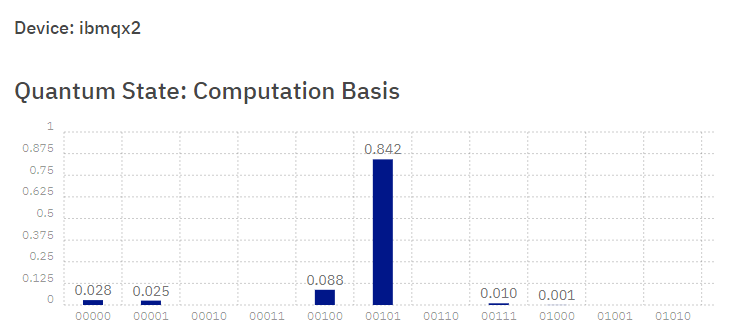
可以看到这个第一位和第二位同时为零的概率是比较小的,但是也不是零(这是由于量子计算机的误差造成的)。 - 常数函数的情况下,这个实验就比较傻了。常数的含义就是不随输入变化,所以整个过程就相当于量子从初态经历了两个Hadamard们就直接输出了。而两个Hadamard门的作用就相当于啥都不做,因此就直接输出初态0了。
所以反向思考,Deutsch-Jozsa算法还真的是很简单的,符合量子纠缠效应的直觉。
参考文献
【1】.《量子计算与量子信息》Michael A. Nielsen
【2】.《量子力学》列文.朗道
【3】.《量子力学原理》P.A.M. Dirac
发表评论