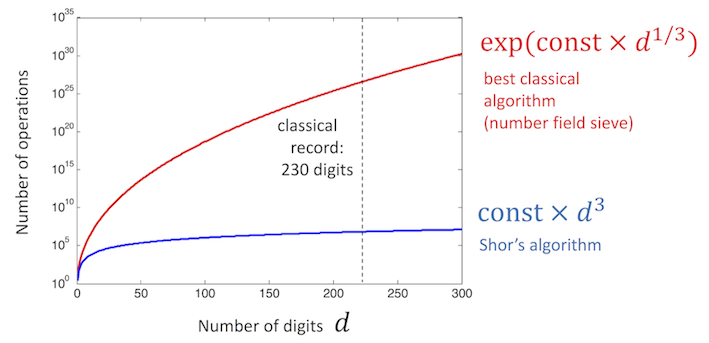
秀尔算法(Shor's algorithm)是一种非常著名的量子算法,甚至可以说是量子计算的一块金字招牌了。Shor's algorithm可以在多项式时间内完成大整数质因数分解。所以Shor's algorithm从诞生之时,就和以RSA算法为根基的加密技术形成了不可调和的矛盾。2001年,IBM的研究小组使用Shor's algorithm完成了15 = 3×5这个整数分解运算 。时至今日,快20年过去了,量子计算机没有摧毁RSA。未来这一天来临的时候,希望我们已经准备好了。下图是,经典大数分解和秀尔算法的复杂度对比。
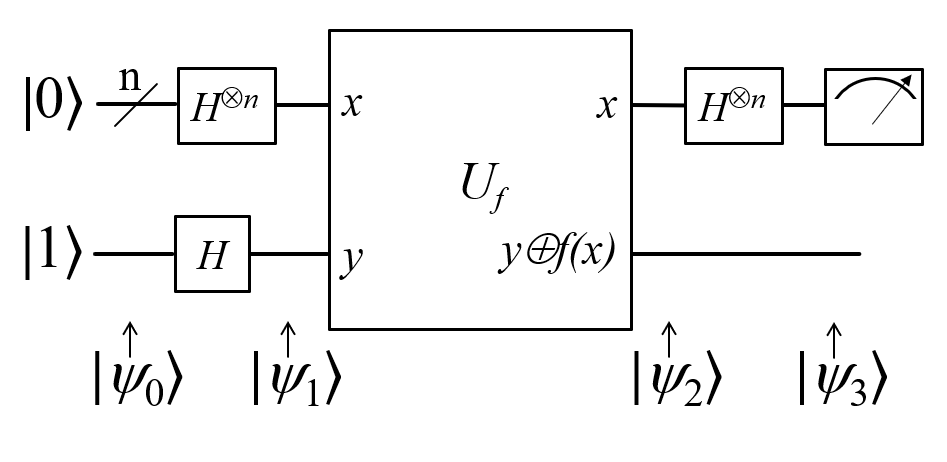
Shor算法的整体流程
完整的Shor算法是需要经典计算机和量子计算机协作完成的。其中量子计算机实现一个周期查找的函数,经典计算机负责整个算法流程的控制,以及调用量子算法。
首先、还是表达一下Shor's algorithm的问题描述:给定一个合成数N�… 【查看更多】
最新评论