本文出自:【InTheWorld的博客】 (欢迎留言、交流)
量子相位估计算法
量子相位估计算法(Quantom Phase Estimation)也称作量子特征值估计算法,是一个比较基本的算法。它的作用直观说来就是来估计一个酉变换的特征值。由于酉矩阵拥有一个性质:酉矩阵的特征值都是模为1的复数。所以对酉矩阵而言,其特征值和相位基本是对等的(因为模长已经确定了)。
量子傅里叶变换
在量子相位估计算法中,需要使用到量子傅里叶反变换。因此,我们简单了解一下量子傅里叶变换的相关知识。经典的离散傅里叶变换作用于一个复向量(x_{0}, x_{1},\cdots,x_{N-1}),并把它映射到另一个向量(y_{0}, y_{1},\cdots,y_{N-1}),其映射关系如下:
y_{k}=\frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} {x_{j}e^{-2\pi ijk/N}}
与其相对应的傅里叶反变换为:
x_{j}=\frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} {y_{k}e^{2\pi ijk/N}}
与上面类似, 量子傅里叶变换作用在量子态上,记为{\displaystyle |x\rangle =\sum _{i=0}^{N-1}x_{i}|i\rangle },并把它映射到量子态{\displaystyle \sum _{i=0}^{N-1}y_{i}|i\rangle }上,而其映射规则在基态上的定义为:
|j\rangle \longrightarrow \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} e^{2\pi ijk/N}|k\rangle
量子傅里叶变换的张量积表示如下所示:
{\displaystyle QFT(|x_{1}x_{2}\ldots x_{n}\rangle )={\displaystyle \frac {1}{\sqrt {N}}}\bigotimes _{j=1}^{n}(|0\rangle +e^{2\pi i[0.x_{j}x_{j+1}\ldots x_{n}]}|1\rangle )}
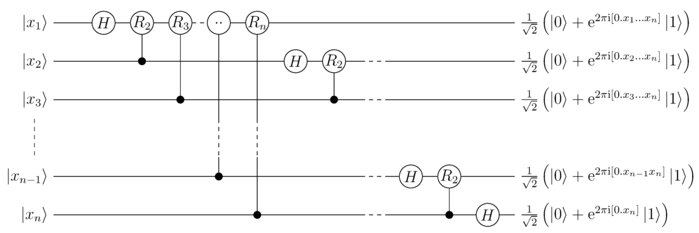
这个公式看起来其实挺直观的,量子傅里叶变换的作用就是根据输入,改变输出量子比特的相位。如果你觉得这个公式都不够简单,那QFT的量子线路应该会让你满意。
上图中的H就是Hadamard门,R_{m}叫做控制相位门。R_{m}对应于如下的酉变换:
R_{m} = \begin{bmatrix} 1 & 0 \\ 0 & e^{2\pi i/2^{m} } \end{bmatrix}
量子傅里叶反变换是量子傅里叶变换的逆过程,考虑量子计算都是可逆过程,量子傅里叶反变换的过程其实也非常好理解了。事实上,量子傅里叶反变换的量子线路就是把QFT的量子线路反过来。
相位估计算法理论
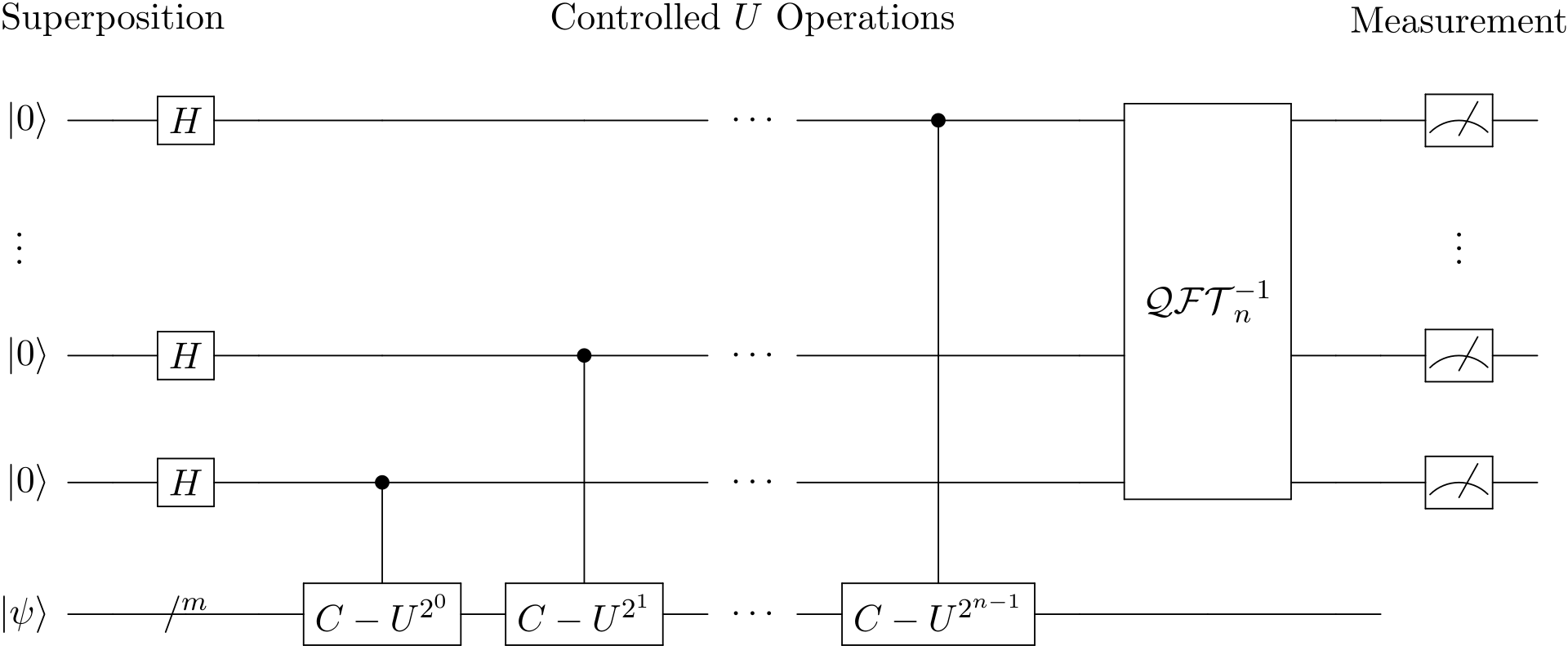
首先给出量子相位估计算法的线路图如下所示:
相位估计算法的线路可以分为两个部分,量子傅里叶变换之前的部分和之后的部分(包含Inverse QFT)。
如前文所说,相位估计算法所解决的问题是这样的:U是一个作用于m个量子比特的酉算子,U存在一个特征向量\vert \psi \rangle,也即{\displaystyle U|\psi \rangle =e^{2\pi i\theta }\left|\psi \right\rangle ,0\leq \theta <1}。然后,我们想找到特征向量|\psi\rangle对应的特征值{\displaystyle e^{2\pi i\theta }},也等价于找到相位\theta。这也是该算法名字的由来。
以下是算法流程:
- \vert 0 \rangle^{\bigotimes n}\vert \psi \rangle; 初始化状态
- \longrightarrow\dfrac{1}{\sqrt{2^n}} \displaystyle\sum_{j=0}^{2^n-1} {\vert j \rangle} {\vert \psi \rangle}; 使用Hadamard门生成叠加态
- \longrightarrow\dfrac{1}{\sqrt{2^n}} \displaystyle\sum_{j=0}^{2^n-1} {\vert j \rangle} {U^{j}} {\vert \psi \rangle} = \dfrac{1}{\sqrt{2^n}} \displaystyle\sum_{j=0}^{2^n-1} {e^{2\pi i j \theta}} {\vert j \rangle} {\vert \psi \rangle};
这一步主要是通过"控制U变换",并利用特征向量的性质。 - \longrightarrow {\vert \widetilde{\phi_{\psi}} \rangle} {\vert \psi \rangle};
这一步主要是应用傅里叶反变换。 - \longrightarrow \widetilde{\phi_{\psi}};
这一步就是测量上部分寄存器的值,估计出相位值\theta。
关于估计误差的计算,这里先略过了,相关资料上都有过程,先偷个懒了。
相位估计算法实例
接下来基于IBM量子计算平台,来完成简单的算法验证。首先考虑如下这个U门,
U= \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}
这个矩阵实际就是对应于泡利-X门,它实现的就是逻辑非。容易计算,这个矩阵有两个特征值,一个是+1,一个是-1。特征值+1对应的标准化特征向量是\frac {|0\rangle +|1\rangle} {\sqrt 2},特征值-1对应的标准化特征向量是\frac {|0\rangle -|1\rangle} {\sqrt 2}。
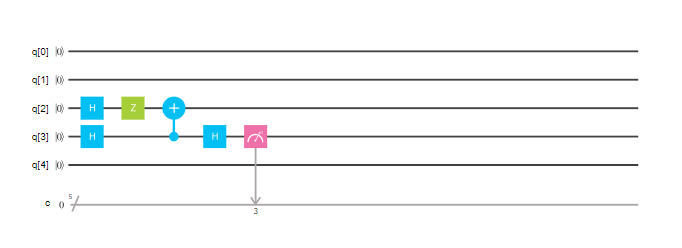
这个量子线路的q[2]相当于第二个寄存器(和特征向量相关的),q[3]相当于第一个寄存器(和测量相关的)。初态|0\rangle经过Hadamard门会变换为\frac {|0\rangle +|1\rangle} {\sqrt 2},然后再经过泡利-Z 门,就变成了\frac {|0\rangle -|1\rangle} {\sqrt 2}。所以,量子相位估计算法预期应该计算出-1这个特征值,对应于相位就是二进制0.1倍的2 \pi,也即\pi。
q[3]为1的概率为81.9%,所以说量子计算机基本找到了对应的相位。虽然例子有点简单了,但是验证了算法的可行性。这篇文章就先到这了!
参考文献
【1】.《量子计算与量子信息》Michael A. Nielsen
【2】.《量子力学》列文.朗道
【3】.《量子力学原理》P.A.M. Dirac
【4】. IBM量子计算实验平台

Good!wawu