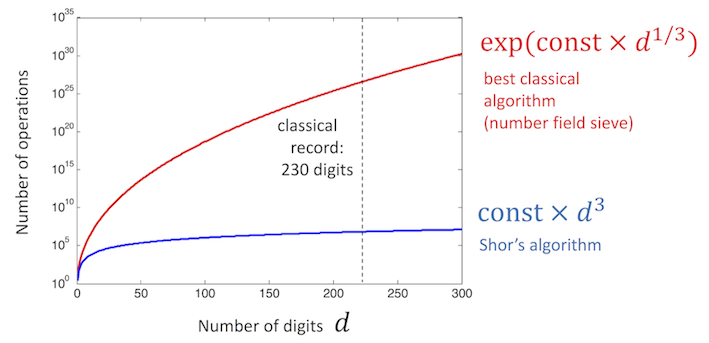
秀尔算法(Shor's algorithm)是一种非常著名的量子算法,甚至可以说是量子计算的一块金字招牌了。Shor's algorithm可以在多项式时间内完成大整数质因数分解。所以Shor's algorithm从诞生之时,就和以RSA算法为根基的加密技术形成了不可调和的矛盾。2001年,IBM的研究小组使用Shor's algorithm完成了15 = 3×5这个整数分解运算 。时至今日,快20年过去了,量子计算机没有摧毁RSA。未来这一天来临的时候,希望我们已经准备好了。下图是,经典大数分解和秀尔算法的复杂度对比。
Shor算法的整体流程
完整的Shor算法是需要经典计算机和量子计算机协作完成的。其中量子计算机实现一个周期查找的函数,经典计算机负责整个算法流程的控制,以及调用量子算法。
首先、还是表达一下Shor's algorithm的问题描述:给定一个合成数N,找到整数p在1和N之间且不包含1和N,并且N整除于p。
- 选择任意数字a < N
- 计算gcd(a, N)。可以使用辗转相除法来计算。
- 若gcd(a, N) \not = 1(不等于,这里不等号渲染有问题),则我们有了一个N非平凡的因数,因此这部分结束了。否则,利用下面的周期查找子程序(Period-finding subroutine,使用量子计算机完成)来找出下面这个函数的周期r:
f(x)=a^{x} {mod} N
换句话说,找出a在{Z} _{N}里面的阶 r,或者最小的正整数r令 f ( x + r ) = f ( x )。
- 若r是奇数,回到第一步。
- 若a^{ r /2} ≡ -1 (mod N),回到第一步。否则,计算gcd(a^{r/2}+1, N)与gcd(a^{r/2}-1, N),并验证他们是不是分别是N非平凡的因数。成功则分解完成。
第三个步骤中,周期查找函数是使用量子计算机完成的。这里暂且不分析这一部分,而关注于整体流程。第一个步骤就是遍历小于N的整数;第二步其实就是碰碰运气,如果a和N的最大公约数不是1,那就是运气好,算法直接结束了;如果最大公约数是1,则调用周期查找子程序计算f(x)=a^{x} {mod} N这个函数的阶数r,mod N就是以N为模的取模运算。
因为f ( x + r ) = f ( x ),而且f ( 0 ) = 1 mod N,因此可得:
f ( 0 ) = f (0+ r )=a^{r} mod N =1mod N
a^{r}-1=0 modN
如果r为偶数,而且a^{ r /2}不等于-1,则可得:
(a^{r/2}+1)(a^{r/2}-1)=0 modN
观察上面的等式可以很容易发现,(a^{r/2}+1)(a^{r/2}-1)和N存在不是1的最大公约数,也即(a^{r/2}+1)或者(a^{r/2}-1)与N非1的最大公约数。通过辗转相除法即可计算出来,然后验证这两个最大公约数是不是N的因子即可。如果是的话,算法就成功了。
整个算法的充分性,其实是比较明显的,因为最终都会验证结果是不是N的因子。算法的必要性,即是不是一定能找到质因子,我其实还没理解清楚,这里先略过了。接下来就是Shor算法的量子部分,即前文说的Period-finding subroutine。
周期查找算法(Period-finding algorithm)
周期查找算法的作用就是求f(x)=a^{x} {mod} N这个函数的周期。查找周期的前提是周期存在,这个函数的周期存在吗?欧拉对这个问题做过证明,有如下结论:gcd ( y, N ) = 1 ,按 Euler 定理,周期 r 一定存在。
周期查找算法其实本质上是特殊情况的相位估计算法变种(如果对相位估计算法,可以看看我前面相位估计的文章),整体的算法流程如下:
- \vert 0 \rangle\vert 0 \rangle; 初始化状态
- \longrightarrow\dfrac{1}{\sqrt{2^t}} \displaystyle\sum_{x=0}^{2^t-1} {\vert j \rangle} {\vert 0 \rangle}; 使用Hadamard门生成叠加态
- \longrightarrow\dfrac{1}{\sqrt{2^t}} \displaystyle\sum_{j=0}^{2^t-1} {\vert x \rangle} {\vert f(x) \rangle} \approx \dfrac{1}{\sqrt{r2^t}} \displaystyle \sum_{l=0}^{r-1} \sum_{x=0}^{2^t-1} {e^{2\pi i lx / r}} {\vert x \rangle} {\vert \hat f(l) \rangle};
这一步主要是通过"控制U变换",其中U{\vert x \rangle}{\vert y \rangle} = {\vert x \rangle}{\vert y \bigoplus f(x) \rangle}。 - \longrightarrow \dfrac{1}{\sqrt{r}} \sum_{l=0}^{r-1} {\vert \widetilde{l / r} \rangle} {\vert \hat f(l) \rangle};
这一步主要是应用傅里叶反变换。 - \longrightarrow { \widetilde{l / r} };
这一步就是测量上部分寄存器的值。 - \longrightarrow {r};
通过连分数算法计算r的值。
其中,第三步使用了控制U门,而且引入新的表示态:
{\vert \hat f(l) \rangle} = \dfrac{1}{\sqrt{r}} \displaystyle \sum_{x=0}^{r-1} {e^{-2\pi i lx / r}} {\vert x \rangle}
其实就是f(x)傅里叶变换之后的态,由于2^t不一定是周期r的整倍数,所以步骤三有一个约等号。此外,由于随机性,l是有很多可能取值的。因此有人可能会质疑如果l是r的整数倍,则连分数算出的r是有问题的。但这个其实不用担心,和r互质的会更多,所以从概率来讲,正确的r会很高概率地被发现。
本来是打算每个算法都做一个线路实现的,可是Shor算法很难搞,这里就只能略过了。这篇水完,量子计算方面应该会暂时告一段落了,毕竟还有太多事情要做。而且写的这些东西,我也不满意,毕竟是现学现卖了,准备之后有时间修改一下。
参考文献
【1】.《量子计算与量子信息》Michael A. Nielsen
【2】.《量子力学》列文.朗道
【3】.《量子力学原理》P.A.M. Dirac
【4】. ETHZ讲义
很认真了,加油!哈哈
谢谢庆伟!我是初学,好些地方都是一知半解的状态。
看不懂,感觉很厉害,
哈哈哈,为什么要把shor算法译成秀儿算法。。。